Editor’s Note: Kenya Overton and Andrew Kuck, Neag School of Education doctoral students in the Department of Curriculum and Instruction, prepared the following rapid research brief with the Center for Education Policy Analysis, Research, and Evaluation (CEPARE)
Society will be recovering from the impact of the COVID-19 pandemic for years to come. However, its impact on student learning is particularly consequential. School closures and other changes brought on by the pandemic caused disruptions in our schools, which for many students led to a decrease in standardized mathematics scores (Agostinelli, 2022). One such change may have been a reversion to traditional instructional methods due to the rapid transition schools made to remote learning. Moldavan and colleagues (2021) found that urban secondary math teachers during the pandemic reported not knowing how to effectively integrate technology into their practice. Additional research shows (An et al., 2021) that 65% of teachers surveyed used a teacher-centered approach of video lectures, while only 23% used a student-centered approach of inquiry-based learning when teaching during the pandemic. The negative consequences of these disruptions, exacerbated by economically disadvantaged students’ limited digital access to virtual lessons, may persist for children until they reach adulthood (Agostinelli et al., 2022).
Educators and the public may be tempted to focus primarily on what students cannot do, benchmarks not met as in years past, and aim efforts towards “catching students up.” However, research indicates that “catching students up” – through compressed content, grade retention, and enhanced Response To Intervention (RTI) – is largely ineffective in helping students who are “behind” (Allensworth et al., 2020). Instead, improving students’ mathematics learning involves high-quality instruction – a student-centered approach that is emotionally and cognitively demanding. This suggests that teachers concentrate on what students can do by capitalizing on the assets they bring to the classroom and not dwell excessively on their perceived “learning loss.”
As students shift back to in-person learning, it is essential for educators to shift back to student-centered teaching. This brief offers guidance to facilitate this shift – or shift back – by highlighting secondary math-specific, researched-based pedagogical practices that center students in the classroom.
The Centrality of Student Engagement in Mathematics Learning
Mathematics learning and achievement follow from student engagement, which must be deliberately and strategically fostered (Watt, 2017). Student-centered teaching emphasizes engagement, recognizing that when students are not engaged, content coverage is largely ineffective (Allensworth et al., 2020). Because student engagement is multi-faceted, teaching for engagement must consider the multiple ways students can be engaged. Specifically, high-quality instruction that engages students emotionally and cognitively leads to more student-centered learning (Allensworth et al., 2020).
Figure 1 shows a set of math-specific, secondary-focused strategies for emotional and cognitive engagement. This brief details ways teachers can foster students’ emotional engagement by using Culturally Relevant Pedagogy (CRP). It further outlines how teachers cognitively engage students by using the Standards of Mathematical Practices, formative assessment, rich mathematical tasks, and technology. Although not an exhaustive list of strategies, the following strategies were noted repeatedly in research studies and can be implemented immediately.
Emotional Engagement
Environmental factors that support emotional engagement can help students value academic learning (Watt, 2017). Cultivating an environment that allows students to make mistakes can lead them to find “uncommon methods of solutions that can promote their fluency, flexibility, and originality in mathematics” (Bicer, 2021, p. 270). Research further recommends that teachers encourage students to take intellectual risks and share their mathematical ideas with others to increase cognitive flexibility in problem solving (Sriraman, 2009). Moreover, when students engage in mathematical discussions with their peers, they make new connections to learning. Celebrating growth, in addition to achievement, and providing multiple opportunities and flexible ways to show mastery are additional approaches teachers can implement immediately to create an emotionally engaging environment (Seda et al., 2020).
Emotionally engaging students also involves understanding what assets they bring to school. When teachers recognize the wealth of unique characteristics (i.e., students’ cultural heritage, personal experiences, social interests, etc.) students bring to the classroom, they can leverage those characteristics to the students’ advantage. As Gutierrez (2018) points out, math content is not independent of personal identity. Instead of assuming that mathematics is identity-neutral, teachers can analyze how the mathematics curriculum fails to take into account students’ backgrounds and use Culturally Relevant Pedagogy (CRP) to produce students who achieve academic success while affirming their cultural identity and growing their political consciousness (Ladson-Billings, 1995a). For educators who do not share the same cultural knowledge or experiences of their students, as is common in the state of Connecticut and elsewhere (Blanco, 2021), Seda et al. (2020) suggest the following strategies:
- Honor student identity – when teachers acknowledge the racial and ethnic identities of their students, they are better able to design mathematical tasks that are relevant to students’ experiences.
- Use resources that portray people of diverse backgrounds favorably – omitting the contributions of people of diverse backgrounds in math curricular materials sends the message to students that only people of European descent are successful in mathematics.
- Use active teaching strategies – active instructional strategies that engage students in real life and genuine problems can both motivate students and tap into their cultural experience.
Educators who focus on students’ assets instead of their deficiencies can better emotionally engage students (Goffney et al., 2018), resulting in students who are invested in what they are learning. When students are able to bond with peers in supportive environments to engage in mathematical tasks designed to reflect their lived experiences, they can connect how mathematics can be used to solve problems in their everyday lives. Students perform better when they do not feel pressured to leave their “true selves at the door” (Nordell, 2021).
Cognitive Engagement
Cognitive engagement – students striving to solve intellectual problems (Watt, 2017) – is equally important. Academic challenges are crucial and a reflection of the quality of tasks designed for a lesson. Cognitively engaging students requires the teacher to know what a proficient math student looks like, design appropriate tasks, then assess students to gauge students’ learning and inform further instruction.
The Standards for Mathematical Practice (SMPs) describe behaviors of proficient math students. The daily inclusion of SMPs in the classroom fosters students’ meaningful engagement in learning mathematics (Selling, 2016).
Envisioning a Mathematically Proficient Student: The Standards for Mathematical Practices
Using mathematics involves skillful processes to tackle complex problems; simply knowing math topics does not necessarily equip students to effectively use mathematics. The Common Core State Standards for Mathematics (CCSSM) Mathematical Practices (SMPs) describe eight core practical mathematical techniques and skills that mathematicians use.
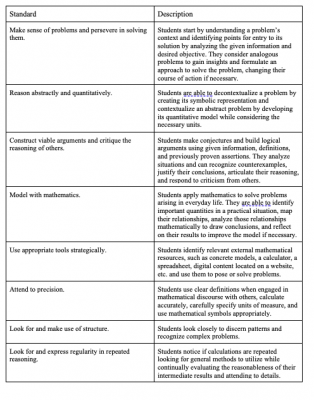
Developing mathematically proficient students involves tasks that promote students’ engagement with these mathematical practices. Integrating these strategies into classrooms not only enables teachers to foster students’ mathematical creativity, but can also promote mathematical equity by allowing all learners access to cognitively engaging instruction (Bicer, 2021).
Developing mathematically proficient students involves tasks that promote students’ engagement with these mathematical practices. Integrating these strategies into classrooms not only enables teachers to foster students’ mathematical creativity, but can also promote mathematical equity.
Designing Tasks that Nurture Mathematical Creativity
Although creativity is more commonly associated with the arts and humanities, researchers acknowledge its importance in STEM-related disciplines (Neuman, 2007).One way to do this is by designing tasks that nurture mathematical creativity (Boaler, 2015). Mathematical creativity is the student’s ability to generate original mathematical ideas, processes, or products by discerning and using acceptable mathematical patterns and models (Bicer, 2021). Educators can cultivate mathematical creativity in their students by developing students’ cognitive flexibility – the ability to activate and modify his/her thought processes as the demands of a task change (Krems, 1995). This can unlock students’ unique ways of solving open-ended mathematical tasks. Activities that foster mathematical creativity are: problem-solving using open-ended problems, problem-posing, and modeling activities (Bicer, 2021).
Problem solving – engaging tasks for which the solution is unknown (NCTM, 2014) – has a strong correlation with mathematical creativity and is identified as one of its best indicators (Sriraman, 2009). The best problem solving tasks that cultivate creativity are open-ended problems – problems that do not specify clearly what is being asked, thereby providing opportunities for students to explore multiple interpretations for various solutions (Bicer, 2021). Students’ creativity in mathematics can be fostered through culturally relevant open-ended problems that allow students to freely apply their imaginations to find novel mathematical ideas and solutions. When students engage in creative problem-solving tasks, it requires them to apply prior learned mathematical rules and procedures to generate original solutions that strengthen comprehension and the interconnectedness of mathematical ideas (Bicer, 2021). Additionally, open-ended problems cultivate a learning environment that promotes diversity of thought as students hear the mathematical ideas, reasoning, and justifications of others (Hiebert et al., 2000).
Problem-posing – the production or reformulation of mathematical problems (Silver, 1994) – requires reasoning and reflection that enables students to look beyond the surface level of content and deepen their mathematical understanding. Whether structured – generating mathematical problems according to a specific scenario – or free, problem posing should be implemented by teachers before, during, and after the problem-solving process. When teachers give students opportunities to create and answer their own mathematical problems, a level of curiosity and enthusiasm appears in students that encourages them to appreciate math’s beauty and not just see it as a set of memorized rules and procedures.
Mathematical modeling – the process of creating models to solve complex problems in a real-world context (The Common Core State Standards, 2010) – provides opportunities for teachers to elicit students’ creative thinking processes by forcing students to select the appropriate mathematics to investigate. Modeling tasks support students’ ability to create, execute, evaluate, and refine various solution methods of given problems. Since mathematical modeling activities enable students to use their prior knowledge to construct new mathematical knowledge and provide teachers with insights into student thought processes, implementing mathematical modeling activities into classroom instruction has multiple benefits (Bicer, 2021).
In her book Mathematical Mindsets, Boaler (2015) provides the following example to model how activities that foster mathematical creativity appear in practice:
In this task, both the solution and the solution strategy are unknown. Students use their own creativity to investigate possible solutions. While the answer is not entirely subjective, multiple solutions are possible. The problem is therefore open enough to be explored in multiple ways, but rigorous enough to require mathematical justification. This task also provides an interesting opportunity to stimulate further problem-posing. Additionally, because no strategy is suggested, students can be encouraged to develop their own mathematical models for arriving at a solution.
As students engage in the problem-solving process, they will inevitably make mistakes. Recall that a supportive class culture that leverages mistakes into learning opportunities is emotionally engaging and helps to develop students’ cognitive engagement and math proficiency.
Formative Assessments
Formative assessment–the systematic process of gathering evidence about student learning and thinking – is a third strategy that can support cognitive engagement (Lildejahl, 2021; NCTM, 2014) and has been identified as one of the most powerful practices to support student learning (Black & Wiliam, 2009; Hattie, 2012). Designing rich mathematical tasks and nurturing creativity for cognitive engagement require that teachers have an intimate knowledge of their students’ capabilities. One teaching practice recommended by the National Council of Teachers of Mathematics (NCTM, 2014) is to “elicit and use evidence of student thinking” (p. 53). Formative assessment helps, as it has been shown to be more effective in improving student achievement than benchmark assessments (Wiliam, 2011). The data produced help identify students’ current learning level so educators can adapt lessons accordingly, thereby increasing students’ engagement.
Teachers can implement formative assessment successfully in their classrooms and maximize opportunities for gathering data by following its four core elements:
- identify gaps between students’ current learning level and the desired educational goal,
- provide feedback that guides students to improve their learning,
- collaborate with students in developing a shared understanding of what is needed to move learning forward, and
- articulate subgoals for a learning progression toward the ultimate goal (Heritage, 2007).
Additionally, knowing the range of formative assessments techniques enables teachers to align them effectively with instructional goals. Some strategies that teachers can use in daily planning and instruction are; observations, questioning, “show me” activities – students demonstrating what they are learning – and exit tasks (Fennell et al., 2015). Observations, questioning, and “show me” activities are used to guide that day’s lesson, while responses to exit tasks assess progress towards learning goals to influence planning for future lessons. The empirical evidence showing formative assessments’ effectiveness in improving student learning (Black et al., 2010) suggests that teachers recognize them as an inseparable part of the teaching process and a valuable process that yields actionable information about students’ learning – not just “another thing” being externally imposed upon them.
Strategic Use of Technology
Technology is often used to engage students, whether by choice, or – in the case distance learning – out of necessity. To mitigate the impact of missed in-person instruction during the pandemic, teachers and students had to quickly transition from face-to-face instruction to a distance learning model, which was only possible through the use of technology. Therefore, this policy brief would be remiss if it did not provide research-based insight on how technology impacts students’ learning of mathematics. As teachers structure their classrooms to foster emotional and cognitive engagement, it is important to acknowledge that technology can both deepen issues of equity and enhance instructional practices (Moldavan et al., 2021) and should be used strategically.
When technology in the classroom is effective, it usually has a very specific role. For example, Hegedus and colleagues (2015) studied a classroom that used computer software to model algebraic functions. The software was used as a tool to enrich instruction, not replace it. Student performance improved as a result of this qualitatively different learning experience. A result corroborated by a meta-analysis conducted by Li and Ma (2010), who found that computer technology was an effective instructional resource when combined with a constructivist teaching approach.
Too often, unfortunately, technology is not used to aid student problem solving, but to teach the same content through a different medium. When technology is used in this way, there is a danger that students are engaging with the technology, but not with the underlying mathematics. In a study conducted by Perry and Steck (2015), students using an interactive geometry app were rated by themselves and their teachers as more engaged, but they did not actually learn any more geometry. When technology is not used judiciously, students can become superficially engaged, but not emotionally or cognitively engaged. As Parkay (2014) puts it, “technology cannot be grafted onto existing curricula; it must be integrated thoughtfully.”
This raises the question of whether computer software can be used to “catch students up” who are below grade-level due to the pandemic. Programs like Aleks and Edmentum’s Exact Path promise to help students master difficult content, with minimal teacher instruction. While this can be a tempting supplement or alternative to traditional instruction, the research on these programs is mixed. For instance, Edmentum’s Exact Path self-guided curriculum – when used to supplement traditional curriculum in middle school – has been shown to raise student test scores (Randel, 2018). However, the gains reported thus far have been small. In a study of high school students, the self-guided Aleks curriculum also raised student test scores, but only when used as a supplement to teacher instruction (Sun, et al., 2021). When used as a replacement for classroom-based instruction, the Aleks curriculum produced results that were equivalent. These results suggest that such programs may provide a reasonable alternative to classroom-based instruction – if necessary – but that they should not be expected to accelerate students’ learning when used in isolation.
Other studies provide further evidence that software is minimally effective in helping students “catch up”. In a recent meta-analysis, Ran and colleagues (2021) found that educational computerized games and programs that offer continuous practice on a stream of math skills do not increase achievement for low-performing students – even when the computerized programs were adaptive and iterative. Moreover, the same study found that the ability of computer technology to aid low-performing students decreases with grade level, with effects sometimes disappearing in high school – a result that had been previously observed (Li et al., 2010). Ultimately, the most effective technology interventions for raising math achievement are computer technologies used to “design and create advanced and appealing problem-solving activities or learning experiences” (Ran et al, p. 144). Such interventions are difficult to implement without teacher involvement. In other words, emotional and cognitive engagement is difficult to achieve with technology alone; existing technology falls short of this goal and is almost always more effective when supplemented by classroom-based instruction.
By sparking enthusiasm and using CRP, teachers can create classroom environments that emotionally engage students to learn, while using the SMPs, formative assessments, rich mathematical tasks, and technology to cognitively engage them.
Conclusion
The evidence presented outlines a clear approach on how teachers can focus their efforts for math achievement and alleviate the negative impact of the Covid-19 pandemic on math proficiency. By sparking enthusiasm and using CRP, teachers can create classroom environments that emotionally engage students to learn, while using the SMPs, formative assessments, rich mathematical tasks, and technology to cognitively engage them. This student-centered approach to instruction is not new, but is all the more important as we work to re-engage students in mathematics classrooms in the wake of (and ongoing impact of) the pandemic. Student-centered approaches also continue to be supported by research. In the rush to “catch students up,” we often end up leaving those students behind (Allensworth et al., 2020). The recommendations outlined in this brief suggest a less frenetic approach, driven not by time-specific benchmarks but by understanding students and engaging them in authentic mathematics – an approach that is ultimately more effective.
This CEPARE Rapid Research Brief was supported by a grant from the American Educational Research Association. Faculty with relevant expertise advised the author throughout the preparation of this brief and reviewed it in advance of publication.
CEPARE produces high-quality research, evaluation, and policy analysis that informs leaders and policymakers on a range of pressing issues, with a particular focus on enhancing social justice and equity across p-20 educational settings in Connecticut and beyond. CEPARE produced this Rapid Research Brief as part of the SETER Alliance, which aims to strengthen and support learning opportunities in Connecticut’s Alliance districts. Learn more about CEPARE cepare.uconn.edu. Access the PDF VERSION (including all references and appendices).
Kenya Overton is a current doctoral student in the Neag School of Education at the University of Connecticut. Having earned her BA and MS in Mathematics from Westfield State College and the University of Mississippi respectively, and 6th Year in Ed Leadership from UConn, Kenya is passionate about ensuring that racially oppressed groups have access to a high quality mathematical education. Prior to pursuing her Ph.D. in Secondary Mathematics Education, Kenya devoted nearly 20 years in public education as an administrator, teacher, and mentor in schools across the country, including states like; Connecticut, Tennessee, New York, and Massachusetts. She has also taught mathematics at the Community College and University levels. Her research interests include: organizational structures in public secondary schools that promote Black math achievement, developing equity-minded math educators, and empowering students in math through Hip-Hop pedagogy.
Andrew Kuck is a doctoral student in the Neag School of Education at the University of Connecticut. He earned a BS from Grand Valley State University in Michigan, and an MA in teaching from Valparaiso University in Indiana. Prior to pursuing his Ph.D., Andrew taught secondary math in Indiana, Illinois, and Massachusetts. His research interests include preservice teacher preparation and mathematical writing. He currently lives in Boston with his wife.
